Dalam matematika, khususnya bidang analisis numerik, metode galerkin merupakan metode yang digunakan untuk
mengubah masalah operator kontinu (seperti persamaan
differensial)
ke masalah diskret. Dalam prinsipnya, metode ini mirip penerapannya dengan metode
variasi ke ruang
fungsi dengan mengubah parsamaannya ke formulasi
lemah. Yang
secara khusus menerapkan beberapa batasan pada ruang fungsi untuk menggolongkan
ruang pada suatu himpunan terbatas dari basis fungsi. Seringkali pada
penggunaannya, metode Galerkin menyajikan juga metode approksimasi yang biasa
digunakan pada umumnya, seperti metode Petrov-Galerkin atau metode
Ritz-Galerkin.
Pendekatan
berharga oleh matematikawan Rusia Boris
Galerkin. Sejak
keindahan metode Galerikin terungkap dalam cara yang sangat abstrak dari studi
mereka, maka pertama kali kita akan memberikan abstrak turunannya. Pada
akhirnya, kita akan memberikan contoh untuk penggunaannya.
Contoh-contoh metode Galerkin adalah:
- Metode elemen berhingga
- Metode elemen pembatas untuk menyelesaikan persamaan
integral
- Metode
sub ruang Kyrlov
Misalkan
kita memasukkan metode Galerkin pada sebuah masalah abstrak yang merupakan
suatu formulasi
lemah
pada ruang Hilbert yaitu V, jika diketahui 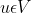
sehingga untuk setiap

maka
&space;=&space;f(v))
adalah
benar. Sekarang ) adalah
bentuk bilinear (penjelasan yang eksak atas
adalah
bentuk bilinear (penjelasan yang eksak atas ) akan
ditentukan selanjutnya) dan f adalah operator linear pembatas pada V.
Pilih
sub ruang
akan
ditentukan selanjutnya) dan f adalah operator linear pembatas pada V.
Pilih
sub ruang 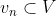 dengan
dimensi yang lebih kecil (sebenarnya, kita akan mengasumsikan bahwa indeks n
menujukkan dimensinya) dan memecahkan masalah yang perhitungkan. Jika diketahui
dengan
dimensi yang lebih kecil (sebenarnya, kita akan mengasumsikan bahwa indeks n
menujukkan dimensinya) dan memecahkan masalah yang perhitungkan. Jika diketahui 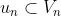
dan untuk setiap
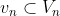
maka :
Kita akan menyebut persamaan ini sebagai persamaan Galerkin.
Dengan catatan bahwa persamaan ini tidak dapat diubah dan hanya ruangnya yang
dapat diubah.
Hal ini merupakan sifat mendasar yang membuat
analisis matematika dari metode Galerkin sangat jelas. Karena 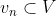
,
kita
dapat menggunakan 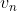 sebagai vector dalam persamaan awal. Substitusi persamaan
yang kedua, kita dapati ortogonalitas Galerkin untuk galat
sebagai vector dalam persamaan awal. Substitusi persamaan
yang kedua, kita dapati ortogonalitas Galerkin untuk galat
Sekarang, 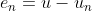 adalah
galat antara solusi masalah awal u dan persamaan Galerkin
adalah
galat antara solusi masalah awal u dan persamaan Galerkin 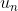 secara berturut-turut.
secara berturut-turut.
Karena tujuan dari metode Galerkin adalah membentuk
sistem persamaan linear, maka kita membangun bentuk matriksnya, sehingga dapat
digunakan untuk menghitung solusi dengan program computer. Misal 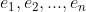
basis untuk
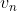 Maka
hal ini cukup untuk menguji coba persamaan Galerkin, sebagai contoh: Diketahui
Maka
hal ini cukup untuk menguji coba persamaan Galerkin, sebagai contoh: Diketahui 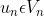
sehingga
Kita
akan mengembangkan 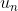 menjadi
basis seperti ini,
menjadi
basis seperti ini, .png) dan
memasukkannya kedalam persamaan di atas, sehingga diperoleh
dan
memasukkannya kedalam persamaan di atas, sehingga diperoleh
untuk i = 1, . . . , n.
Dalam
persamaan sebelumnya, sebenarnya merupakan sistem persamaan linear 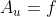 dimana
dimana
.
Dalam
kaitannya dengan definisi dari matriks
entry, matriks dari persamaan Galerkin adalah simetrik jika dan hanya jika
bentuk bilinear ) adalah
simetrik.
adalah
simetrik.
Analisis dari Metode Galerkin
Sekarang, kita akan membatasi diri kita pada
bentuk bilinear simetrik, yaitu
Karena
ini bukan benar-benar sebuah batas dari metode Galerkin, aplikasi dari teori
standar ini menjadi sangat mudah. Selanjutnya, metode Petrov-Galerkin dibutuhkan dalam kasus non-simetrik. Analisis
dari metode ini dihasilkan dalam dua langkah. Yang pertama, kita akan
menunjukkan bahwa persamaan Galerkin adalah well-posed
problem
menurut Hadamard dan oleh karena itu kita mengakui persamaan ini
sebagai solusi yang tunggal. Pada langkah kedua, kita mempelajari pendekatan
sifat dari solusi Galerkin 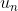
.
Analisi ini kebanyakan akan mengacu pada dua sifat dari
bentuk bilinear, yakni:
- Pembatasan:
untuk setiap
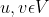 adalah
benar bahwa
adalah
benar bahwa untuk konstanta C > 0.
untuk konstanta C > 0.
- Eliptisitas:
untuk setiap setiap
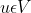

Menurut teorema Lax-Milgram, ada dua kondisi implikatif
well-posedness dari masalah awal dalam formulasi
lemah. Semua
kaidah dalam bagian berikut ini akan dinormalisasikan untuk pertidaksamaan
benar di atas (kaidah ini sering disebut juga kaidah energy).
.png) dan
memasukkannya kedalam persamaan di atas, sehingga diperoleh
dan
memasukkannya kedalam persamaan di atas, sehingga diperoleh 
 solusi
Galerkin
solusi
Galerkin 





.png)
.png)










